Bell State Generator

This notebook examines a lossy bell-state generator, similar to that shown in Figure 1 of [BBGS+21].

First, the required modules are imported.

import matplotlib.pyplot as plt
import numpy as np

import lightworks as lw
from lightworks import emulator

The circuit for this can be built in the following way, in which modes 0-3 are the inputs, all containing a single photon and modes 4-7 are ancilla. This is not a physical circuit, and instead some re-arrangement of the modes would be required.

circ = lw.PhotonicCircuit(8)

# Assigned per-element loss to 0.05
loss = lw.Parameter(0.05, label="loss")

for i in range(4):
    circ.bs(i, 4 + i, loss=loss)
    circ.ps(i, np.pi / 2)
    circ.bs(i, 4 + i, loss=loss)

circ.bs(4, 5, loss=loss)
circ.ps(4, np.pi / 2)
circ.bs(4, 5, loss=loss)

circ.bs(6, 7, loss=loss)
circ.ps(6, np.pi / 2)
circ.bs(6, 7, loss=loss)

circ.bs(5, 6, loss=loss)
circ.ps(5, 0)
circ.bs(5, 6, loss=loss)

circ.bs(4, 5, loss=loss)
circ.ps(4, np.pi / 2)
circ.bs(4, 5, loss=loss)

circ.bs(6, 7, loss=loss)
circ.ps(6, np.pi / 2)
circ.bs(6, 7, loss=loss)

circ.bs(5, 6, loss=loss)
circ.ps(5, 0)
circ.bs(5, 6, loss=loss)

circ.display()

Sampling

In this case, we use the heralding function to select a particular measurement outcome from the ancilla modes. We then use the min_detection option to ensure that 4 photons total leave the circuit.

in_state = lw.State([1, 1, 1, 1, 0, 0, 0, 0])
herald_func = lambda s: s[4] == 1 and s[5] == 1 and s[6] == 0 and s[7] == 0

N_rep = 100000
sampler = lw.Sampler(
    circ,
    in_state,
    N_rep,
    post_selection=herald_func,
    min_detection=4,
    random_seed=10,
)

backend = emulator.Backend("slos")
results = backend.run(sampler)

states, counts = [], []
for s, c in results.items():
    states.append(s[:4])
    counts.append(c)

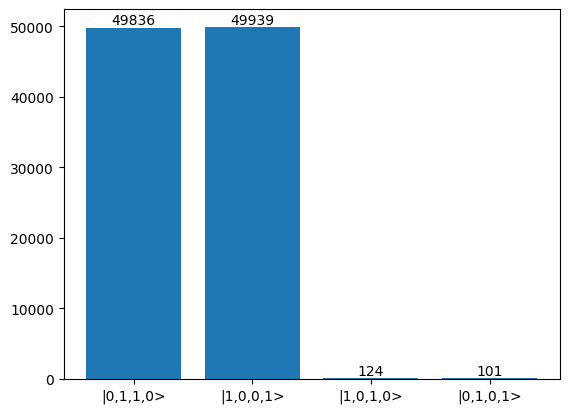
As can be seen from the plot below, for the measurement pattern [1,1,0,0] on the ancilla modes, we usually get the states |1,0,0,1> and |0,1,1,0> across the other 4 modes, which is as expected. If we convert this to dual rail encoded qubits, then this corresponds to the state |01> + |10>, which is a bell state, showing the generator works correctly. We can also see how loss in the circuit leads to some errors presenting themselves in the operation.

bars = plt.bar(range(len(states)), counts)
plt.bar_label(bars, counts)
plt.xticks(range(len(states)), states)
plt.show()